Coefficient Asymptotics in SageMath
Benjamin Hackl • September 19, 2023

Extracting Coefficient Diagonals of Rational Multivariate Generating Functions in SageMath

Joint work with Andrew Luo, Stephen Melczer, Jesse Selover, Elaine Wong
(Interactive) Software Demo • ÖMG Meeting @ Graz
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

Overview: sage_acsv

  • Input: multivariate, rational, combinatorial generating function \[ F(\mathbf{z}) = \sum_{i_1, i_2, ..., i_d \geq 0} f_{i_1, ..., i_d} z_1^{i_1} \cdots z_d^{i_d}, \] and direction vector $\mathbf{r} = (r_1, ..., r_d) \in \mathbb{N}^d$
  • Output: asymptotic expansion for diagonal $f_{n \mathbf{r}}$ for $n\to\infty$

A practical example: binomial coefficients

\begin{align*} F(x, y) &= \frac{1}{1 - x - y}\\ &\fragment{0}{= 1 + (x+y) + (x+y)^2 + (x + y)^3 + (x+y)^4 + \ldots}\\ &\fragment{1}{= \sum_{k, \ell \geq 0} \binom{k + \ell}{k} x^{k} y^{\ell}} \end{align*}
  • $\mathbf{r} = (1, 1)$ → $[x^n y^n] F(x, y) = \binom{2n}{n}$ $\sim \frac{4^n}{\sqrt{\pi n}}$
  • $\mathbf{r} = (19, 9)$ → $[x^{19n} y^{9n}] F(x, y) = \binom{28n}{19n}$

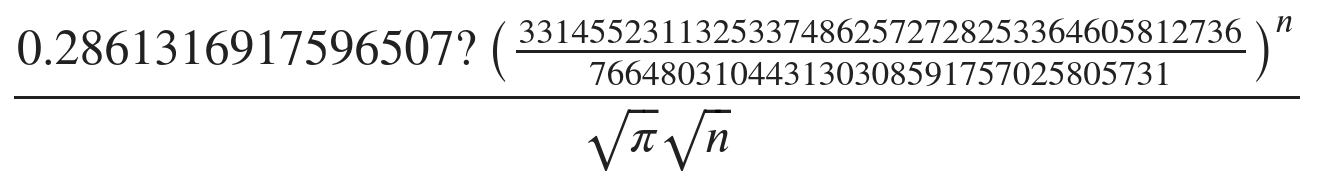
How does it work?

  • $F(\mathbf{z}) = G(\mathbf{z})/H(\mathbf{z})$, with $G$ and $H$ (multivariate) polynomials
  • Multivariate CIF: $f_{n\mathbf{r}} = \frac{1}{(2\pi i)^d} \int_{\mathcal{C}} \frac{G(\mathbf{z})}{H(\mathbf{z})} \frac{d\mathbf{z}}{\mathbf{z}^{n \mathbf{r} + 1}}$
  • Under "mild" conditions on $H$ ($H(0)\neq 0$; $H$ and all partial derivatives do not vanish simultaneously; finitely many smooth critical points, at least one of which is minimal; phase Hessian non-singular at these points) "(smooth) critical minimal points" determine asymptotics cf. [Pemantle-Wilson], [Baryshnikov-Pemantle] ...

Reminder: univariate case, $d = 1$

  • Via partial fraction decomposition: \[ F(z) = \frac{G(z)}{H(z)} = \sum_{w\in S} \frac{p_w(z)}{(1 - z/w)^{\alpha_w}} \]
  • ... and after extracting coefficients: \[ [z^n] F(z) = \sum_{w\in S} \sum_{j=0}^{\alpha_w - 1} c_{j, w} w^{-n} n^{j} \]
  • Largest contribution from "minimal" singularities (smallest modulus)

Trouble in higher dimensions!

  • Singular points no longer isolated, $H(\mathbf{z}) = 0$ describes algebraic variety $\mathcal{V}$
  • "Minimal" singularities (on border of domain of convergence): $\mathcal{V} \cap \partial\mathcal{D}$
  • Do all of the (infinitely many?) $w\in \mathcal{V}\cap \partial\mathcal{D}$ contribute to coefficient asymptotics? 🤔

One step at a time: a simple growth bound

$T(\mathbf{w})$ ... polytorus with radii $w_1$, $w_2$, ..., $w_d$

  • Via multivariate version of Cauchy's integral formula: \[ f_{n\mathbf{r}} = \frac{1}{(2\pi i)^d} \oint_{T(\mathbf{w})} F(\mathbf{z}) \frac{d\mathbf{z}}{z_1^{nr_1 + 1} \dots z_d^{nr_d + 1}} \]
  • Integral bound, let $C_w := \max_{\mathbf{z}\in T(\mathbf{w})} |F(z)| < \infty$: \[ |f_{n\mathbf{r}}| \leq C_w |w_1|^{-nr_1} \cdots |w_d|^{-nr_d} = C_w \exp(h_{\mathbf{r}}(\mathbf{w}) \cdot n), \] with $h_{\mathbf{r}}(\mathbf{w})$ ... "height function"

A simple growth bound (II)

  • Consequence of bound: for $w\in\overline{\mathcal{D}}$ we know
\[ \limsup_{n\to\infty} |f_{n\mathbf{r}}|^{1/n} \leq \exp\Bigl(- \sum_{j=1}^d r_j \log|w_j|\Bigr) = \exp(h_r(\mathbf{w})) \]
  • Where is approximation "best"? → $\min_{w\in\mathcal{V}\cap\partial\mathcal{D}} h_\mathbf{r}(w)$
  • Characterization under suitable conditions (e.g., combinatoriality):
\[ (\nabla_{\log} H)(\mathbf{w}) || \mathbf{r} \quad\iff\quad r_1 w_j H_{z_j}(w_j) - r_j w_1 H_{z_1}(w_1) = 0 \]

Critical points

Definition: A point $w \in (\mathbb{C}\setminus\{0\})^d$ with ...
  • $H(w) = 0$$w\in \mathcal{V}$
  • $r_1 w_j H_{z_j}(\mathbf{w}) - r_j w_1 H_{z_1}(\mathbf{w}) = 0$ for $2\leq j\leq d$$(\nabla_{\log} H)(\mathbf{w}) || \mathbf{r}$
where any $H_{z_j}(\mathbf{w}) \neq 0$ is called smooth critical point.
  • Note: we have "best" asymptotic bounds at critical points.
  • Cauchy integral can be approximated there; points are feasible for saddle point method!

Minimal Points $\cap$ Critical Points

  • Minimal points $w\in \mathcal{V}\cap\partial\mathcal{D}$: integration contour can be deformed arbitrarily close
  • Critical points: "best" asymptotic approximations; saddle point method applicable
  • Thus, minimal critical points are particularly interesting!

Min. Crit. Points: Existence & Contribution

  • Do minimal (smooth) critical points always exist?
    • $F(x, y) = 1/(2 + y - x(1 + y)^2)$ has no critical points ...
    • ... but in combinatorial cases existance is guaranteed!
  • Do non-critical minimal points contribute to asymptotics too?
    • No! Integration contour can be deformed "around" non-critical points (because "height not minimized")

Min. Crit. Points: Toy Example

\[ F(x, y) = \frac{1}{1 - x - y},\qquad \mathbf{r} = (19, 9) \]
\[ H(x, y) = 1 - x - y \stackrel{!}{=} 0 \rightsquigarrow x + y = 1 \]
\[ \nabla_{\log} H(x, y) = \begin{pmatrix} -x \\ -y \end{pmatrix} \bigg|\bigg| \begin{pmatrix} 19\\ 9 \end{pmatrix} \fragment{2}{\rightsquigarrow -9x + 19y = 0} \]
  • Critical point: $\mathbf{w} = (19/28, 9/28)$
  • Exponential "bound": $\limsup_{n\to\infty} \binom{28n}{19n}^{1/n} \leq |w_1|^{-r_1} |w_2|^{-r_2} = \Bigl(\frac{28}{19}\Bigr)^{19} \Bigl(\frac{28}{9}\Bigr)^{9}$

Installation & Demo

Algorithmic Approach

  • Find critical points $\mathbf{w} \in \mathbb{C}_{*}^d$ via $H(\mathbf{w}) = 0$ and $\mathbf{0}\neq \nabla_{\log} H(\mathbf{w}) \| \mathbf{r}$
  • Check which critical points are minimal

Use all-in-one strategyvia [Melczer-Salvy]:

  • Consider system $H(t \mathbf{w}) = 0$, $\nabla_{\log} H(\mathbf{w}) || \mathbf{r}$, encode solutions with Kronecker representationlinear form $u - \kappa \mathbf{z} = 0$, polynomials $P$, $Q_1$, ..., $Q_d$ s.t. $Q_j(u)/P'(u) = z_j$ determine components of solution vector for $u$ iterating through roots of $P$ -- bounded coefficients / degrees!
  • Check positive ($\sim$ Pringsheim!) solutions for $t = 1$
  • Use solutions for $t\in (0,1)$ to eliminate non-min. $\mathbf{w}$

Thank you!