Asymptotic Expansions in SageMath
Benjamin Hackl • November 17, 2022

Software Demo:
Asymptotic Expansions in SageMath

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

Motivation: a story about cutting trees

Joint work with Clemens Heuberger, Sara Kropf, Helmut Prodinger
  • Input: random plane tree of size $n$
  • Procedure: remove all leaves, repeat until tree is deleted
Question: expected tree size after $r\in\mathbb{Z}_{\geq 0}$ iterations?

Cutting a "larger" tree

Tools of the trade: generating functions

  • $\mathcal{T}$ ... class of plane trees; inner nodes $\rightsquigarrow z$, leaves $\rightsquigarrow w$
\[ \mathcal{T} = \text{leaf} + \text{inner node} \times \text{non-empty sequence of } \mathcal{T} \]
\[ T(z, w) = w + z\cdot \frac{T(z, w)}{1 - T(z, w)} \]
\begin{align*} T(z, w) &= \frac{1 - (z-w) - \sqrt{1 - 2(z+w) + (z-w)^2}}{2}\\ &\fragment{4}{= w + wz + wz^2 + w^2 z + wz^3 + 3w^2z^2 + w^3 z + ...} \end{align*}

$[z^n w^k] T(z,w)$ counts # of trees with $n$ inner nodes and $k$ leaves.

Trimming vs Growing Trees

  • From every current leaf: grow $\geq 1$ new leaf
    \[ w \longrightarrow z\cdot \frac{w}{1-w} \]
  • From every inner node: grow $\geq 0$ new leaves before/after every outgoing edge
    \[ z^n w^k \longrightarrow z^n \Big(\frac{1}{1-w}\Big)^{2n+k-1} \]
Combined: $\quad z^n w^k \longrightarrow z^{n+k} w^k \frac{1}{(1-w)^{2n + 2k - 1}}$

Tree Expansion Operator

Combined: $\quad z^n w^k \longrightarrow z^{n+k} w^k \frac{1}{(1-w)^{2n + 2k - 1}}$
  • Note: expansion does not depend on tree shape, only on number of inner nodes and leaves
  • Define linear operator $\Phi$ that expands a tree family, \[ \Phi(f(z, w)) := (1-w) f\bigg(\frac{z}{(1-w)^2}, \frac{zw}{(1-w)^2}\bigg) \]

Iterated tree expansions, and back to cutting

Theorem.
\begin{align*} G_r(z, v) &= \Phi^r(T(zv, wv))|_{w=z}\\ &= \frac{1 - u^{r+2}}{(1 - u^{r+1})(1+u)} T\bigg(\frac{u (1 - u^{r+1})^2}{(1 - u^{r+2})^2} v, \frac{u^{r+1} (1-u)^2}{(1 - u^{r+2})^2} v\bigg) \end{align*} with $z = u/(1+u)^2$ counts trees with respect to both their size ($\rightsquigarrow z$) and their size after $r$ cuts ($\rightsquigarrow v$).
  • Construction of linear, multiplicative $\Psi$, study of $\Psi^r(t)$, $\Psi^r(z)$
  • Recurrences involving Fibonacci polynomials, coordinate transformation $z = u/(1+u)^2$
  • $X_{n,r}$ ... RV for size of tree after $r$ cuts
\[ \mathbb{E} X_{n,r} = \frac{1}{C_{n-1}} [z^n] \frac{u^{r+1}}{(1+u) (1 - u^{r+1})} \]

Asymptotic Expansions in SageMath

Joint work with Thomas Hagelmayer, Clemens Heuberger, Daniel Krenn, ...
  • Want: framework for computations with generalized power series with rigorous control over error terms 
sage: A.<n> = AsymptoticRing('n^QQ', SR, default_prec=4)
sage: (1 + 1/n)^n
e - 1/2*e*n^(-1) + 11/24*e*n^(-2) - 7/16*e*n^(-3) + O(n^(-4))
  • Initial implementation as a Google Summer of Code project in 2015
  • Gradual improvement and refactors over the years
  • $B$-terms (explicitly bounded $O$-terms) in GSoC'21

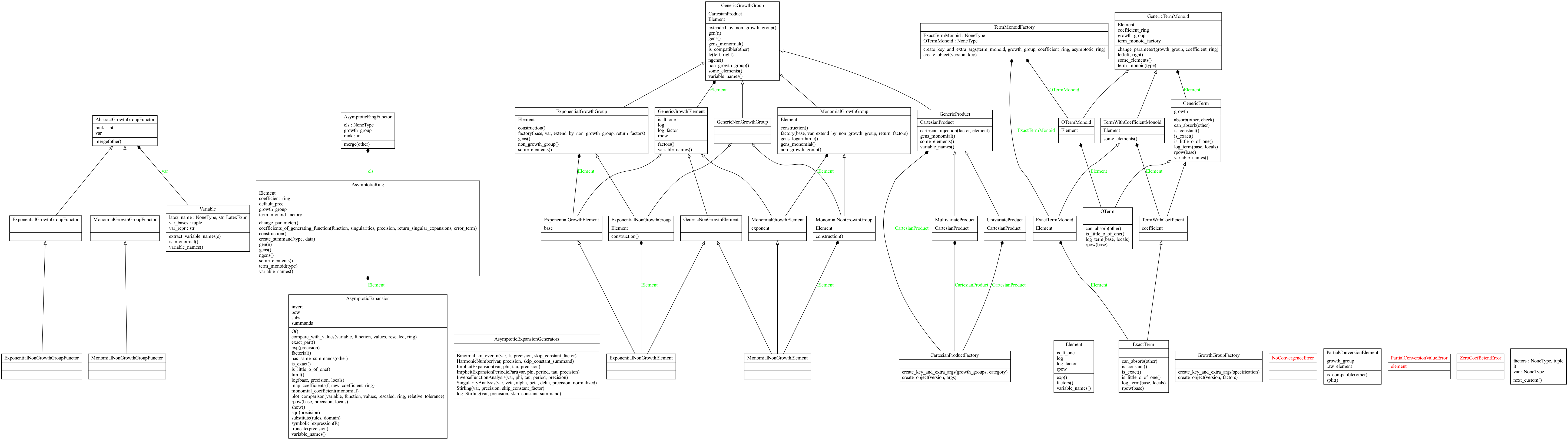
Basic Design Ideas

  • AsymptoticRing $\ni$ AsymptoticExpansion, sum of (partially ordered) terms
  • TermMonoid $\ni$ AsymptoticTerm, summands of the expansion, $42\log(n)^3$, $O(n^{42})$
  • GrowthGroup $\ni$ GrowthElement, holds only the growth
Development principles of SageMath:
  • every (new) class / function needs documentation ...
  • ... and tests!

Interactive Demo

behackl.dev/asy

The average size of $r$-fold cut trees

\[ \mathbb{E} X_{n,r} = \frac{1}{C_{n-1}} [z^n] \frac{u^{r+1}}{(1+u) (1 - u^{r+1})} \] 

>>> catalan_shifted_asy = asymptotic_expansions.Binomial_kn_over_n(n, k=2, precision=3)
>>> catalan_shifted_asy = catalan_shifted_asy.subs(n=n-1) / n
>>> catalan_shifted_asy
1/4/sqrt(pi)*4^n*n^(-3/2) + 3/32/sqrt(pi)*4^n*n^(-5/2) + 25/512/sqrt(pi)*4^n*n^(-7/2) + O(4^n*n^(-9/2))
>>> z_asy = 1/4 * (1 - Z^-1)
>>> u_asy = upsilon(z_asy) + O(Z^-2); u_asy
1 - 2*Z^(-1/2) + 2*Z^(-1) - 2*Z^(-3/2) + 2*Z^(-2) - 2*Z^(-5/2) + O(Z^(-2))
>>> singular_expansion = fast_callable(u^(r+1) / (1 + u) / (1 - u^(r+1)), vars=(u, r))(u_asy, r)
>>> singular_expansion
(1/4/(r + 1))*Z^(1/2) + 1/4*((r + 1)^2 + r + 1)/(r + 1)^2 - 1/2 + (1/2*r - 1/2*((r + 1)^2 + r + 1)/(r + 1) + 1/12*(3*((r + 1)^2 + r + 1)^2/(r + 1)^2 - (2*(r + 1)^3 + 3*(r + 1)^2 + 4*r + 4)/(r + 1))/(r + 1) + 1/2)*Z^(-1/2) + O(Z^(-1))
>>> expectation = singular_expansion._singularity_analysis_(n, zeta=1/4, precision=3) / catalan_shifted_asy
>>> expectation.map_coefficients(lambda t: t.simplify_rational())
(1/(r + 1))*n - 1/6*(r^2 - r)/(r + 1) + O(n^(-1/2))
Theorem.

After $r$ cuts, the average number of remaining nodes is \[ \mathbb{E} X_{n,r} = \frac{n}{r+1} - \frac{r(r-1)}{6(r+1)} + O(n^{-1/2}). \]

Thank you!