Uncovering a Random Tree
 This work is licensed under a Creative Commons
Attribution-NonCommercial-ShareAlike 4.0 International
License.
This work is licensed under a Creative Commons
Attribution-NonCommercial-ShareAlike 4.0 International
License.
The Uncover Process
- Take a random labeled tree with labels $1, 2, \dots, n$
- "Cover" all vertices and edges
- Process: uncover vertex $j$ in step $j$
- Edges are uncovered if both endpoints are uncovered
Motivation: study of coalescent models
Particle coalescence: process on mass clusters; masses $x_i$, $x_j$ merge at rate $x_i + x_j$ (additive coalescent)- Many different models and applications: [Kingman], [Bertoin], [Aldous, Pitman], [Pitman], [Janson], ...
- None of these models capture the behavior of the
uncover process !
What are we interested in?
- number of uncovered edges / clusters
- size of root cluster
- size of largest cluster
Uncovered Edges: Generating Function
Uncovered Edges: Stochastic Process
$(K_j^{(n)})_{1\leq j\leq n}$ ... # of uncovered edges after $j$ uncovered vertices
- with $j$ uncovered vertices, $\binom{j}{2}$ of $\binom{n}{2}$ possible edge positions are uncovered
- there are $n-1$ edges in total, all positions are equally likely
Uncovered Edges: Deviation
- Linearly interpolated, continuous process: $(\tilde K_t^{(n)})_{0\leq t\leq 1}$
- Deviation: subtract mean, rescale. Limiting behavior?
Uncovered Edges: Characterization – Statement
The centered, rescaled, linearly interpolated process \[ Z^{(n)}(t) = \frac{\tilde K_t^{(n)} - t^2 n}{\sqrt{n}} \]
Note: $Z^{\infty}$ is almost a Brownian bridge, $(1-t) W(t/(1-t))$
Uncovered Edges: Characterization – Ingredients
\[ \mathbb{P}\big(\sup_{t\in[0,1]} |Z^{(n)}(t)| \geq C\big) \leq \frac{4}{(C-1)^2} \] For $C\to\infty$: process exceeds $C$ with probability $\to 0$.
Proof: construction of related martingale; application of Doob's $L^p$-inequality.
\begin{align*} \mathbf{K}_{\mathbf{t}n} = \big( K_{\lfloor t_1 n\rfloor}^{(n)}, \dots, K_{\lfloor t_r n\rfloor}^{(n)} \big) \end{align*} \begin{align*} \frac{\mathbf{K}_{\mathbf{t}n} - \mathbb{E} \mathbf{K}_{\mathbf{t}n}}{\sqrt{n}} \xrightarrow[n\to\infty]{d} \mathcal{N} \end{align*}
Proof: construct p.g.f. from $E_n$, \[ P_n = \prod_{i=2}^{n-1} \Big( \frac{1}{n} + \frac{i}{n} z_i + \sum_{h=i+1}^{n-1} \frac{1}{n} z_h \Big), \] sum of multinomial variables! Then: multivariate central limit theorem.
Root Cluster Size: Approach
- $\mathcal{T}^{\bullet}$ ... rooted labeled trees
- $\mathcal{G}$ ... refinement of $\mathcal{T}^{\bullet}$, uncovered vertices are marked with $U$
- $\mathcal{F}$ ... refinement of $\mathcal{G}$, vertices in root cluster marked with $V$
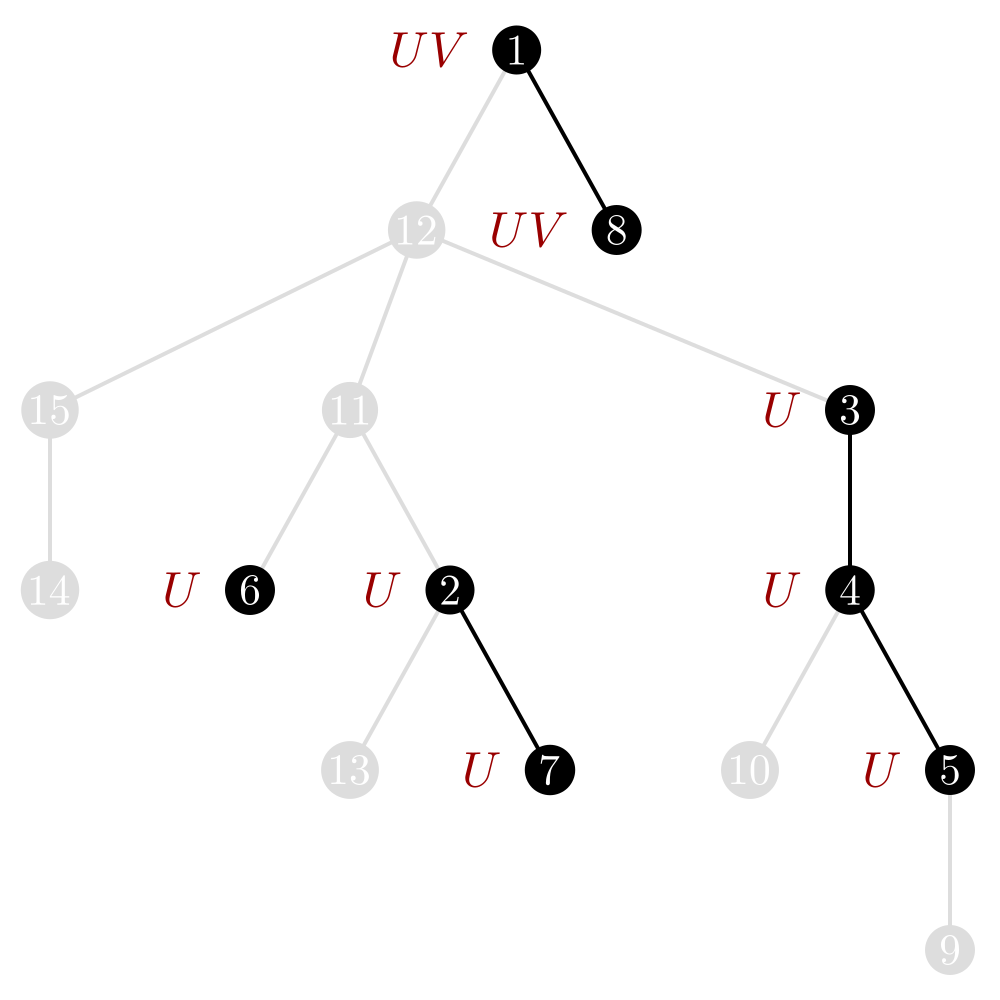
\begin{align*} \mathcal{F} &= \mathcal{Z} \ast \mathrm{Set}(\mathcal{G}) + \mathcal{Z}\times \{U, V\} \ast \mathrm{Set}(\mathcal{F}) \\ \mathcal{G} &= (\mathcal{Z} + \mathcal{Z}\times \{U\}) \ast \mathrm{Set}(\mathcal{G}) \\ \end{align*}
Root Cluster Size: Approach
\begin{align*} \mathcal{F} &= \mathcal{Z} \ast \mathrm{Set}(\mathcal{G}) + \mathcal{Z}\times \{U, V\} \ast \mathrm{Set}(\mathcal{F}) \\ \mathcal{G} &= (\mathcal{Z} + \mathcal{Z}\times \{U\}) \ast \mathrm{Set}(\mathcal{G}) \\ \end{align*}
\[ F = z e^G + zuv e^F \qquad G = z (1 + u) e^G \]
$R_n^{(k)}$ ... root cluster size after $k$ uncovered vertices (out of $n$) \[ \mathbb{E} R_n^{(k)} = \sum_{j=1}^k \frac{j k^{\underline{j}}}{n^j} \]
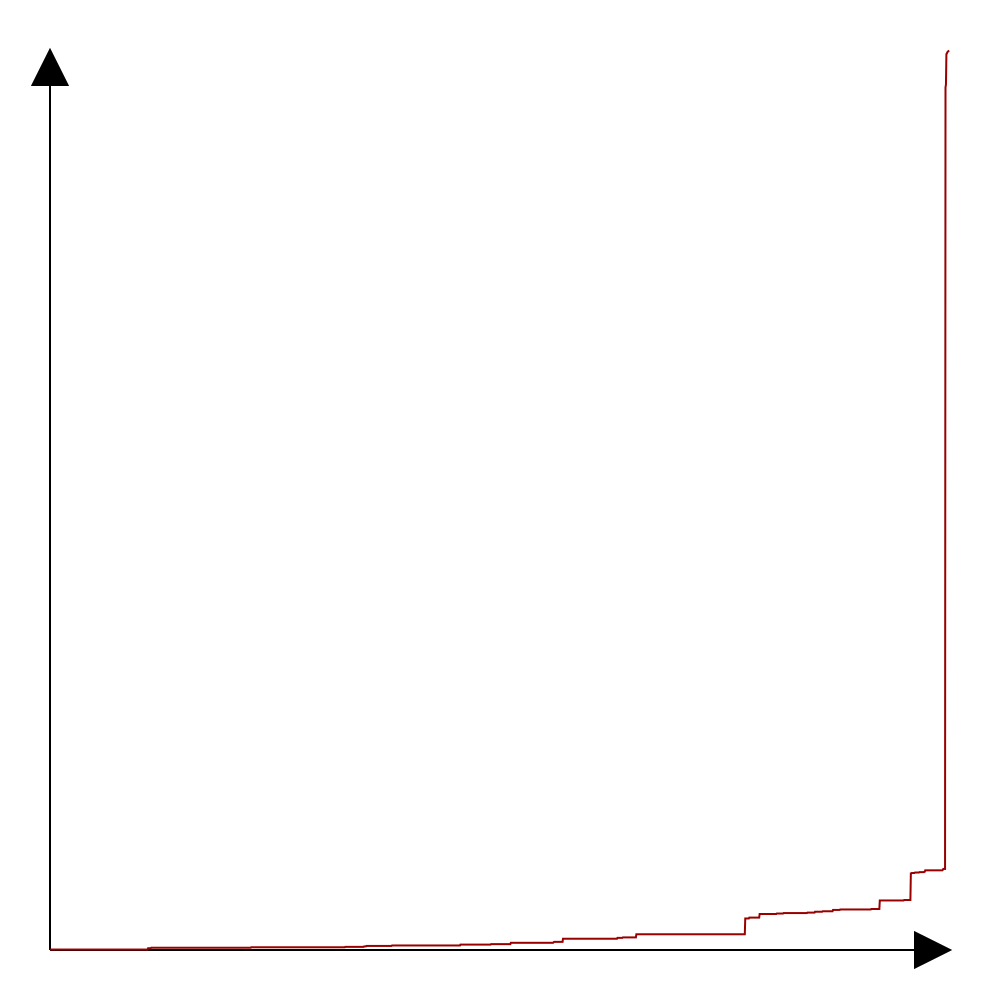
Root Cluster Size: Analysis
\[ \mathbb{E} R_n^{(k)} = \sum_{j=1}^k \frac{j k^{\underline{j}}}{n^j} \fragment{1}{= \int_0^{\infty} (x-1) e^{-x} \big(1 + \frac{x}{n}\big)^k~dx} \]Depending on $k = k(n)$, we find $\mathbb{E} R_n^{(k)} \sim f(n)$, with
$k$ |
$k = o(n)$ |
$k \sim \alpha n$ |
$d=\omega(\sqrt{n})$ $k = n-d$ |
$d\sim c\sqrt{n}$ $k = n-d$ |
$d=o(\sqrt{n})$ $k = n-d$ |
| $f(n)$ | $k/n$ | $\frac{\alpha}{(1 - \alpha)^2}$ | $n^2/d^2$ | $\kappa n$ | $n - d\sqrt{\pi n /2}$ |
Root Cluster Size: Probabilities
Lagrange inversion on $F$ or ...\[ \mathbb{P}(R_n^{(k)} = r) = \begin{cases} 1 - k/n & \text{if } r = 0,\\ r^r (n-k) (n-r)^{k-r-1} \binom{k}{r} n^{-k} & \text{if } 1\leq r\leq k < n,\\ 1 & \text{if } r = k = n. \end{cases} \]
Root Cluster Size: Limiting Behavior
- $k = o(n)$:
$R_n^{(k)} \to 0$ - $k \sim \alpha n$:
$R_n^{(k)} \to R_{\alpha}$ , non-degenerate discrete RV - subcritical, $k = n-d$ with $d = \omega(\sqrt{n})$:
$(d/n)^2 R_n^{(k)} \to \mathrm{Gamma}(1/2, 1/2)$ - critical, $k = n - d$ with $d \sim c\sqrt{n}$:
$R_n^{(k)} / n \to R(c)$ - supercritical, $k = n - d$ with $d = o(\sqrt{n})$:
$(n - R_n^{(k)})/d^2 \to D$
Counting Clusters
- $X_{n, r}^{(k)}$ ... # clusters of size $r$ after uncovering $k$ out of $n$ vertices
- Counting vertices in $T$ w.r.t. clusters: $\sum_{r=1}^{n} r X_{n,r}^{(k)}(T) = k$
- From before: $r n^{n - k - 1} (n-k) (n - r)^{k-r-1}$ special forests
- Cayley's tree formula: $r^{r-2}$ possible clusters, $n^{n-2}$ trees overall
Abel's binomial theorem: $\sum_{r=1}^k \binom{k}{r} r^r (n-r)^{k-r-1} = \frac{k}{n-k} n^{k-1}$
Largest Cluster: Characterization
- subcritical, $k = n - \omega(\sqrt{n})$:
$c_{\max}^{(k)}(T_n)/n \to 0$ in probability, - critical, $k = n- \Theta(\sqrt{n})$: $c_{\max}^{(k)}(T_n)/n$ converges weakly to (non-degenerate) continuous limiting distribution
- supercritical, $k = n-o(\sqrt{n})$: w.h.p. there is a giant component of size $\sim n$
Summary
number of uncovered edges : process mean is $j(j-1)/n$, (rescaled) deviation behaves similar to Brownian bridge-
characterization of
distribution of root cluster size , critical region is $n - \Theta(\sqrt{n})$ uncovered vertices -
analysis of
size of largest cluster in and around critical region of $n - \Theta(\sqrt{n})$ uncovered vertices -
along the way: several
neat combinatorial results (e.g., enumeration of special forests; Abel's binomial theorem, ...)