What can you expect?

A brief history of Manim and its versions

• 3b1b/manim: in development since 2015, until 2018 as single-person^{[Grant Sanderson]} project
• May 2020: Formation of a small community, #1 was merged!
• Since then: ~1050 PRs by over 75 contributors! 🤯

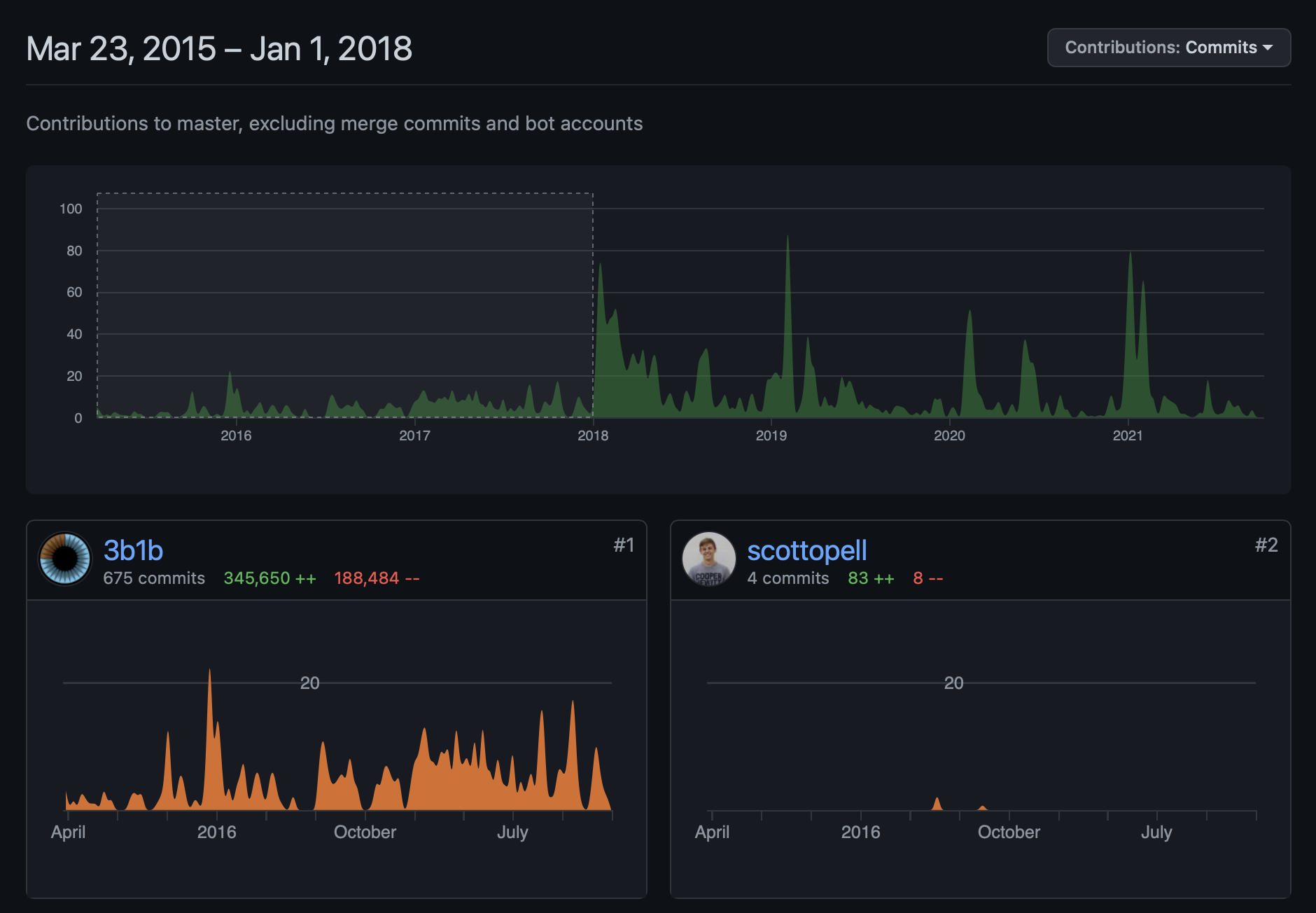
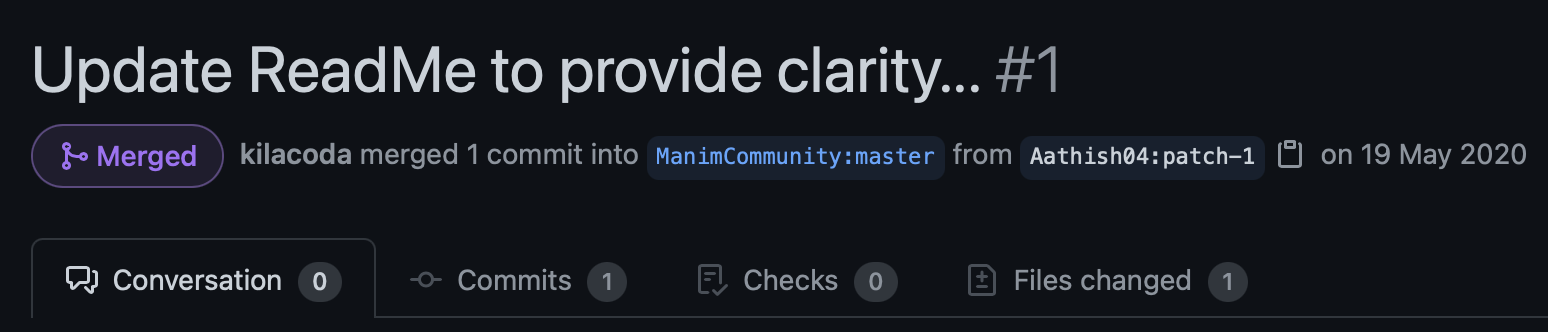
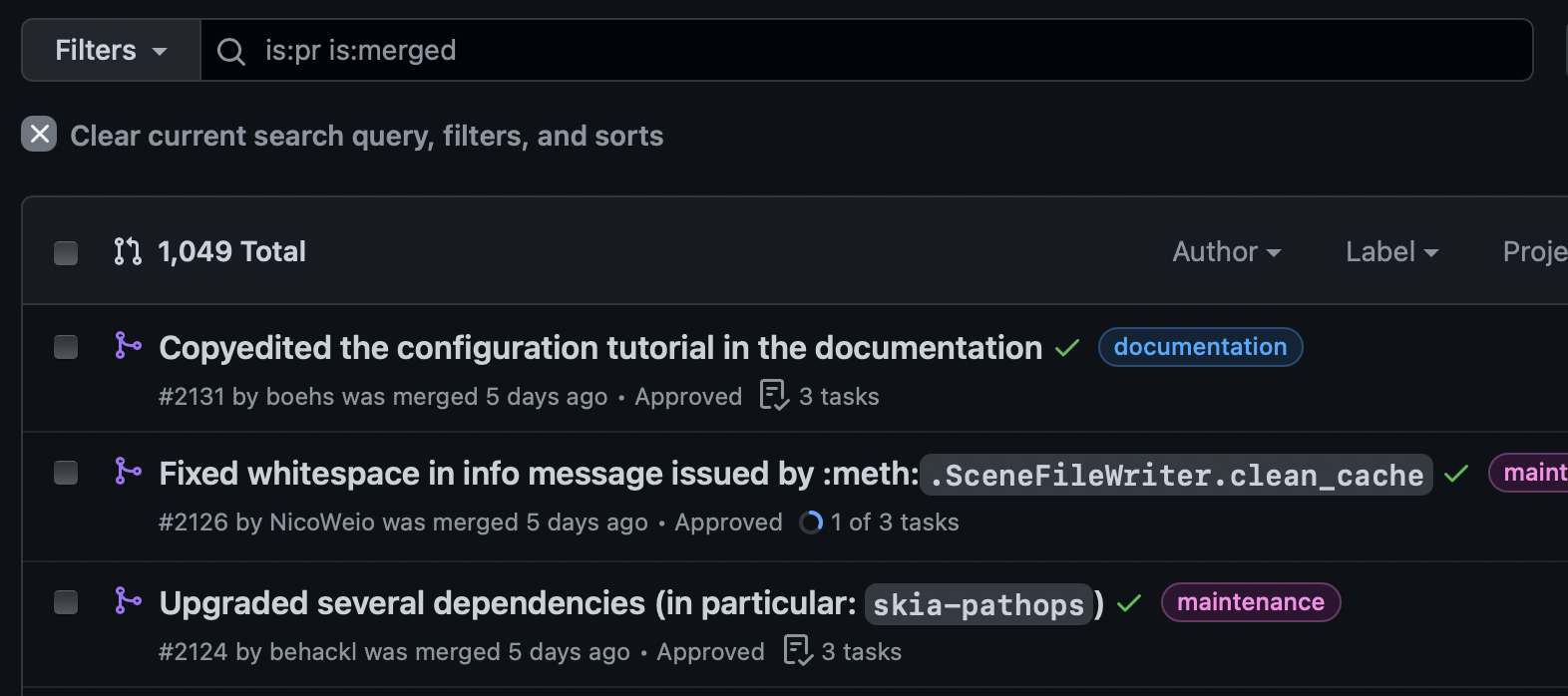
Some more statistics

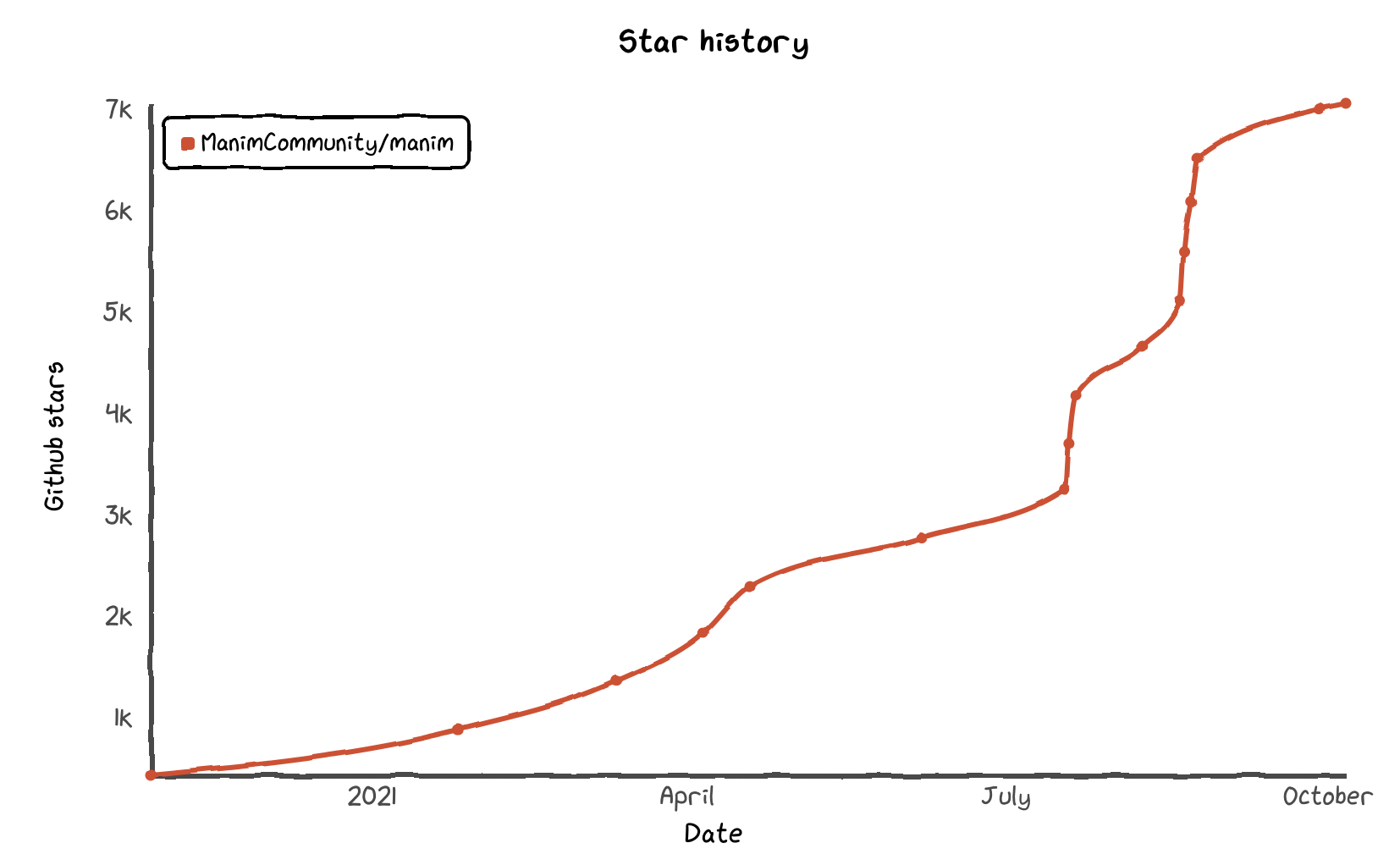
• Daily documentation page visits: 6000–8000!
• Over 13.000 monthly downloads^{[on PyPI]}
• Over 7000 ⭐️ on GitHub

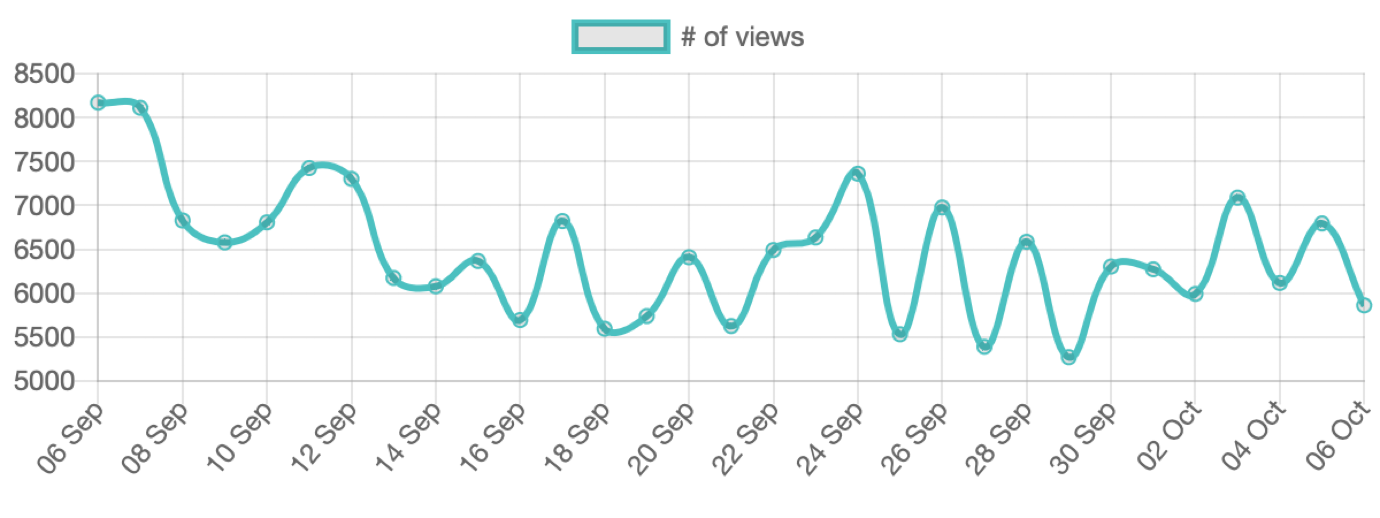
How can you use Manim?

• Today: Online — head to this online environment!
  
  
• Further options:
  • local installation: instructions
  • docker image: manimcommunity/manim:stable

Manim and Jupyter notebooks

• Use arrow keys / mouse to navigate through cells in a notebook, press ▶️ or Shift + Enter to execute cells.
• First step: import Manim. With config some options can be setup, e.g., output video width or log verbosity:

  from manim import *
  
  config.media_width = "80%"
  config.verbosity = "WARNING"

A first animation!

%%manim -qm CircleToSquare

class CircleToSquare(Scene):
    def construct(self):
        blue_circle = Circle(color=BLUE, fill_opacity=0.5)
        green_square = Square(color=GREEN, fill_opacity=0.8)
        self.play(Create(blue_circle))
        self.wait()
        
        self.play(Transform(blue_circle, green_square))
        self.wait()

Positioning Mobjects

• Manim coordinates: 3D coordinate system, by default visible XY plane: $[-7.11, 7.11]\times [-4, 4]$, origin in center of screen.

%%manim -qm HelloCircle

class HelloCircle(Scene):
	def construct(self):
		circle = Circle()
		blue_circle = circle.set_color(BLUE).set_opacity(0.5)
		
		label = Text("A wild circle appears!")
		label.next_to(blue_circle, DOWN, buff=0.5)
		
		self.play(Create(blue_circle), Write(label))
		self.wait()

• Methods: next_to, move_to, shift
• Constants: UP, DOWN, RIGHT, LEFT

The .animate syntax – method animations

• Methods like rotate, scale, move_to modify mobjects.
• These changes can be animated in by using .animate!

%%manim -qm CircleAnnouncement

class CircleAnnouncement(Scene):
	def construct(self):
		blue_circle = Circle(color=BLUE, fill_opacity=0.5)
		announcement = Text("Let us draw a circle.")
		
		self.play(Write(announcement))
		self.wait()
		
		self.play(announcement.animate.next_to(blue_circle, UP, buff=0.5))
		self.play(Create(blue_circle))

The .animate syntax – method animations

• Multiple methods can be applied at once by chaining them.

%%manim -qm AnimateSyntax

class AnimateSyntax(Scene):
	def construct(self):
		triangle = Triangle(color=RED, fill_opacity=1)
		self.play(DrawBorderThenFill(triangle))
		self.play(triangle.animate.shift(LEFT))
		self.play(triangle.animate.shift(RIGHT).scale(2))
		self.play(triangle.animate.rotate(PI/3))

The .animate syntax – method animations

• Caution: .animate works by directly interpolating between initial and target mobject, this can lead to unintended effects.

%%manim -qm DifferentRotations

class DifferentRotations(Scene):
    def construct(self):
        left_square = Square(color=BLUE, fill_opacity=0.7).shift(2*LEFT)
        right_square = Square(color=GREEN, fill_opacity=0.7).shift(2*RIGHT)
        self.play(left_square.animate.rotate(PI),
                  Rotate(right_square, angle=PI), run_time=2)
        self.wait()

Manim and LaTeX

• Full support!
• Note: "\" in Python strings need to be escaped (\\), or a raw string (r"...") needs to be used.

%%manim -qm CauchyIntegralFormula

class CauchyIntegralFormula(Scene):
	def construct(self):
		formula = MathTex(
			r"[z^n]f(z) = \frac{1}{2\pi i}\oint_{\gamma} \frac{f(z)}{z^{n+1}}~dz"
		)
		self.play(Write(formula), run_time=3)
		self.wait()

Manim and LaTeX

• There is syntactic sugar for easier transformations: strings get split according to double braces {{ ... }}.

%%manim -qm TransformEquation

class TransformEquation(Scene):
	def construct(self):
		eq1 = MathTex("42 {{ a^2 }} + {{ b^2 }} = {{ c^2 }}")
		eq2 = MathTex("42 {{ a^2 }} = {{ c^2 }} - {{ b^2 }}")
		eq3 = MathTex(r"a^2 = \frac{c^2 - b^2}{42}")
		self.add(eq1)
		self.wait()
		self.play(TransformMatchingTex(eq1, eq2))
		self.wait()
		self.play(TransformMatchingShapes(eq2, eq3))
		self.wait()

• Specialized transforms: TransformMatchingTex, TransformMatchingShapes

Plotting

%%manim -qm PlotDemo

import numpy as np

class PlotDemo(Scene):
    def construct(self):
        ax = Axes(x_range=[-1, 5, 1], y_range=[-2, 2, 1])
        f = lambda x: np.sin(x*PI) * x/2
        plot = ax.get_graph(f, color=GREEN)
        area = ax.get_area(plot, x_range=[1, 3])
        self.add(ax)
        self.wait()
        self.play(Create(plot))
        self.play(DrawBorderThenFill(area))
        self.wait()

Graphs

%%manim -v WARNING -qm ErdosRenyiGraph

import networkx as nx

nxgraph = nx.erdos_renyi_graph(14, 0.5)

class ErdosRenyiGraph(Scene):
    def construct(self):
        G = Graph.from_networkx(nxgraph, layout="spring", layout_scale=3.5)
        self.play(Create(G))
        self.play(*[G[v].animate.move_to(5*RIGHT*np.cos(ind/7 * PI) +
                                         3*UP*np.sin(ind/7 * PI))
                    for ind, v in enumerate(G.vertices)])
        self.play(Uncreate(G))

Further Resources?

• Documentation: docs.manim.community
• Discord: manim.community/discord
• Development: github.com/ManimCommunity/manim
• Tutorial^{[like this talk but better :-)]} try.manim.community

Thank you!