Down-Steps in Generalized Dyck Paths
Benjamin Hackl • August 17, 2021

Exploring Down-Step Sequences
in Generalized Dyck Paths

Joint work with Andrei Asinowski and Sarah J. Selkirk
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

Motivation

Enumeration of generalized Kreweras walks in the quarter plane:
  • Step set $\{(a, b), (-1, 0), (0, -1)\}$, with $a, b\in \mathbb{Z}_{>0}$
  • Start and end at $(t_x, t_y)$, stay in quarter plane
  • Projections are special Dyck paths!
  • Observe: order of steps $(-1,0)$, $(0, -1)$ between $(a, b)$-steps can be changed, projections stay fixed
  • So, what can we say about down-steps in these projections?

Projected paths — $k_t$-Dyck paths

  • Step set: $\{ (1, k), (1, -1) \}$
  • Start and end on $y=0$, stay weakly above $y=-t$
    Equivalent: start and end on $y=t$, stay weakly above $y=0$
  • For this talk: $0\leq t\leq k$ (path structure changes for $t > k$)

Counting $k_t$-Dyck paths

Proposition.
For $n \geq 0$ and $0\leq t \leq k$, $k_t$-Dyck paths with $n$ up-steps (length $(k+1)n$) are enumerated by generalized Fuss–Catalan numbers \[ C_{n,t} = \frac{t+1}{(k+1)n + t + 1} \binom{(k+1)n + t + 1}{n}. \]
Enumeration is well-known, e.g., via [Mohanty, 1979] or [Krattenthaler, 2015]. One elegant strategy: Cycle Lemma!

Counting $k_t$-Dyck paths

Cycle Lemma. [Dershowitz–Zaks, 1990]
For any sequence of $m$ boxes and $n$ circles ($m \geq kn$), $m-kn$ cyclic shifts are $k$-dominating[all prefixes have #boxes > k #circles].

$k_t$-Dyck path enumeration proof idea: they are bijective to...

  • paths with step set $\{(1, 1), (1, -k)\}$
  • + starting at $(0, -(t+1))$, going to $((k+1)n+t+1, 0)$
  • ... and then to $k$-dominating sequences with $kn+t+1$ boxes and $n$ circles $\rightsquigarrow \frac{m-kn}{m+n} \binom{m+n}{n} = \frac{t+1}{(k+1)n+t+1} \binom{(k+1)n+t+1}{n}$

Counting $k_t$-Dyck paths

  • paths with step set $\{(1, 1), (1, -k)\}$
  • + starting at $(0, -(t+1))$, going to $((k+1)n+t+1, 0)$
  • ... and then to $k$-dominating sequences with $kn+t+1$ boxes and $n$ circles $\rightsquigarrow \frac{m-kn}{m+n} \binom{m+n}{n} = \frac{t+1}{(k+1)n+t+1} \binom{(k+1)n+t+1}{n}$

Counting Down-steps in $k_t$-Dyck paths

  • $s_{n, t, r}$ ... total number of down-steps between $r$-th and $(r+1)$-th up-step in all $k_t$-Dyck paths of length $(k+1)n$ (= $n$ up-steps)
\[ s_{2, 1, 0} = {\color{blue}3}, \quad s_{2, 1, 1} = {\color{lightblue}9},\quad s_{2, 1, 2} = 16 \]

Down-steps before the first up-step

Theorem (Asinowski–H.–Selkirk, 2020+)
The total number of down-steps before the first up-step in all $k_t$-Dyck paths of length $(k+1)n$ is \[ s_{n, t, 0} = \sum_{j=0}^{t-1} C_{n, j}. \]
Proof idea:
  • Mark $j$-th down-step at start of path
  • Cyclic shift: move first $j$ steps to end $\rightsquigarrow$ $k_{t-j}$-Dyck path

Down-steps between 1st and 2nd up-step in $k_0$-Dyck paths

Theorem (Asinowski–H.–Selkirk, 2020+)
The total number of down-steps between the first and second up-step in all $k_0$-Dyck paths of length $(k+1)n$ is \[ s_{n, 0, 1} = \sum_{j=0}^{k-1} C_{n-1, j} = \frac{k}{n} \binom{(k+1)(n-1)}{n-1}. \]
\[ s_{n, 0, 1} = \sum_{j=0}^{k-1} C_{n-1, j} = \frac{k}{n} \binom{(k+1)(n-1)}{n-1} \]
  • Decomposition: "middle segment", from marked step to last return to same level
  • see middle segments as $k_j$-Dyck paths $\rightsquigarrow$ sum,
  • or as family of "elevated paths" $\rightsquigarrow$ binomial coefficient, via [Gu–Prodinger–Wagner, 2010]

Down-steps everywhere else

Theorem (Asinowski–H.–Selkirk, 2020+)
For all $1\leq r\leq n$, the number of down-steps between the $r$-th and $(r+1)$-th up-steps in all $k_t$-Dyck paths of length $(k+1)n$ satisfies \[ s_{n, t, r} = s_{n, t, r-1} + C_{r, t} (s_{n-r+1, 0, 1} - t[r = n]). \]
Some intuition:
  • $r$-marked paths: one marked down-step between $r$-th and $(r+1)$-th up-step
  • $s_{n,t,r}$ counts $r$-marked $k_t$-Dyck paths

Down-steps everywhere else

\[ s_{n, t, r} = s_{n, t, r-1} + C_{r, t} (s_{n-r+1, 0, 1} - t[r = n]) \]
  • $s_{n,t,r-1}$: peak shift bijection
  • Move $r$-th up-step in $(r-1)$-marked path
  • Note: this does not cover $r$-marks below level $-t+k$
  • These correspond to the second summand, use similar "middle segment"-type decomposition

Down-steps and generating functions

  • A separate "guess and prove"-type generating function approach leads to the same results
  • Core observation: with $x = z(1-z)^k$, the generating function enumerating $k_t$-Dyck paths is \[ S_t(x) = \frac{1}{(1-z)^{t+1}} \]
  • Additional advantage: generating function approach allows access to asymptotics of variance!

Down-Step Asymptotics

Theorem (Asinowski–H.–Selkirk, 2020+)
$X_{n, t, r}$ ... random variable, number of down-steps between $r$-th/$(r+1)$-th up-step in uniformly random $k_t$-Dyck path \[ \mathbb{E} X_{n, t, r} = \frac{k}{t+1} \Big(\frac{k^{t+1}}{(k+1)^t} - k + t\Big) + C(r, k, t) + O\Big(\frac{1}{n}\Big) \]
For $r\in\{0, 1, n\}$, \[ \mathbb{V} X_{n, t, r} = \tilde{C}(r, k, t) + O\Big(\frac{1}{n}\Big) \]

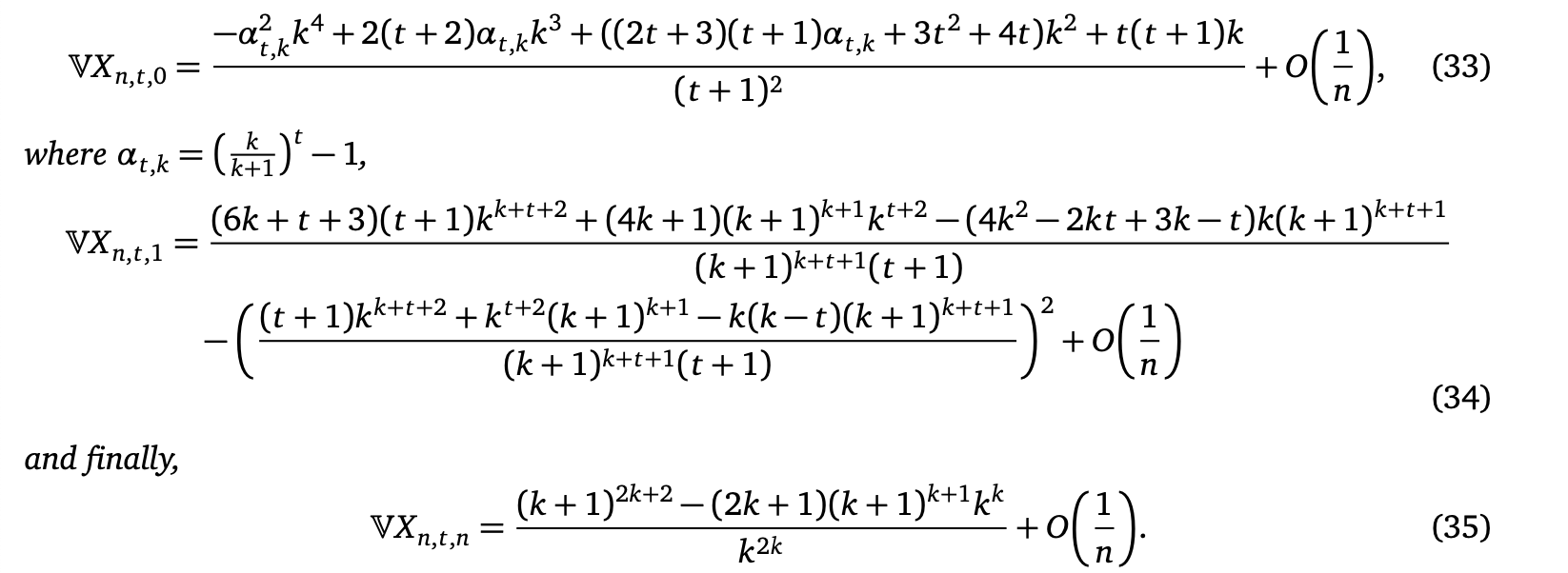
Intermission: Punctured Convolutional Codes

Idea: add redundancy to bitstream to allow detection / correction of transmission errors
  • Compute simple output function per input block
  • Group outputs, delete bits according to "puncture pattern"

Perforation Patterns

  • Perforation patterns can be represented as matrices
  • [Bégin, 1989]: perforation patterns are equivalent iff their matrices are cyclic-column-shift equivalent

From Perforation Patterns to Down-Steps

Theorem (Asinowski–H.–Selkirk, 2020+)
The number of distinct perforation patterns[0/1-matrices] of dimension $(k+1)\times n$ with $n+1$ many 1-entries is \[ \frac{1}{n} \binom{(k+1)n}{n+1} = s_{n, 0, 1}. \]
  • Proof strategy: among all cyclic-column-shifted matrices, only exactly one corresponds to an elevated $k_0$-Dyck path
  • New Cycle Lemma-type result: there is precisely one cyclic permutation of the sequence blocks such that, if a prefix contains at least one 1-entry, we have $k\cdot \# 1 \gt \# 0$

Special case: Yet another Catalan structure!

Equivalence classes of binary $2\times n$-matrices with $n+1$ many 1-entries with respect to the "cyclic column shift"-relation are in bijection to Dyck-paths of length $2n$ (and enumerated by $C_n$).

Summary

  • Motivated by enumeration of generalized Kreweras-walks in the quarter plane
  • Explicit (summation) formulas for number of down-steps in $k_t$-Dyck paths, also generating functions
  • Expected number / variance of number of down-steps between two particular up-steps is $\text{const} + O(1/n)$
  • Via equivalence classes of binary matrices: connection to coding theory
  • New Cycle Lemma-type result for cyclic block shifts (plus yet another interpretation of Catalan numbers!)

Thank you!