Flip-sorting and pop-stacked permutations
Benjamin Hackl • May 20, 2021

Combinatorial aspects of
flip-sorting and pop-stacked permutations

Joint work with Andrei Asinowski, Cyril Banderier, Sara Billey, Svante Linusson.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

Runs and Falls in Permutations

  • Permutation: bijective map $\sigma\colon [n] \to [n]$
  • Run / Fall: consecutive elements getting larger / smaller
1342756
134|27|56
1|3|42|75|6

Flip-sort and the Pop-Stack Operator $T$

  • $T$ ... reverse ("flip") all falls!
  • Repeat until sorted!

$\sigma$

$T(\sigma)$

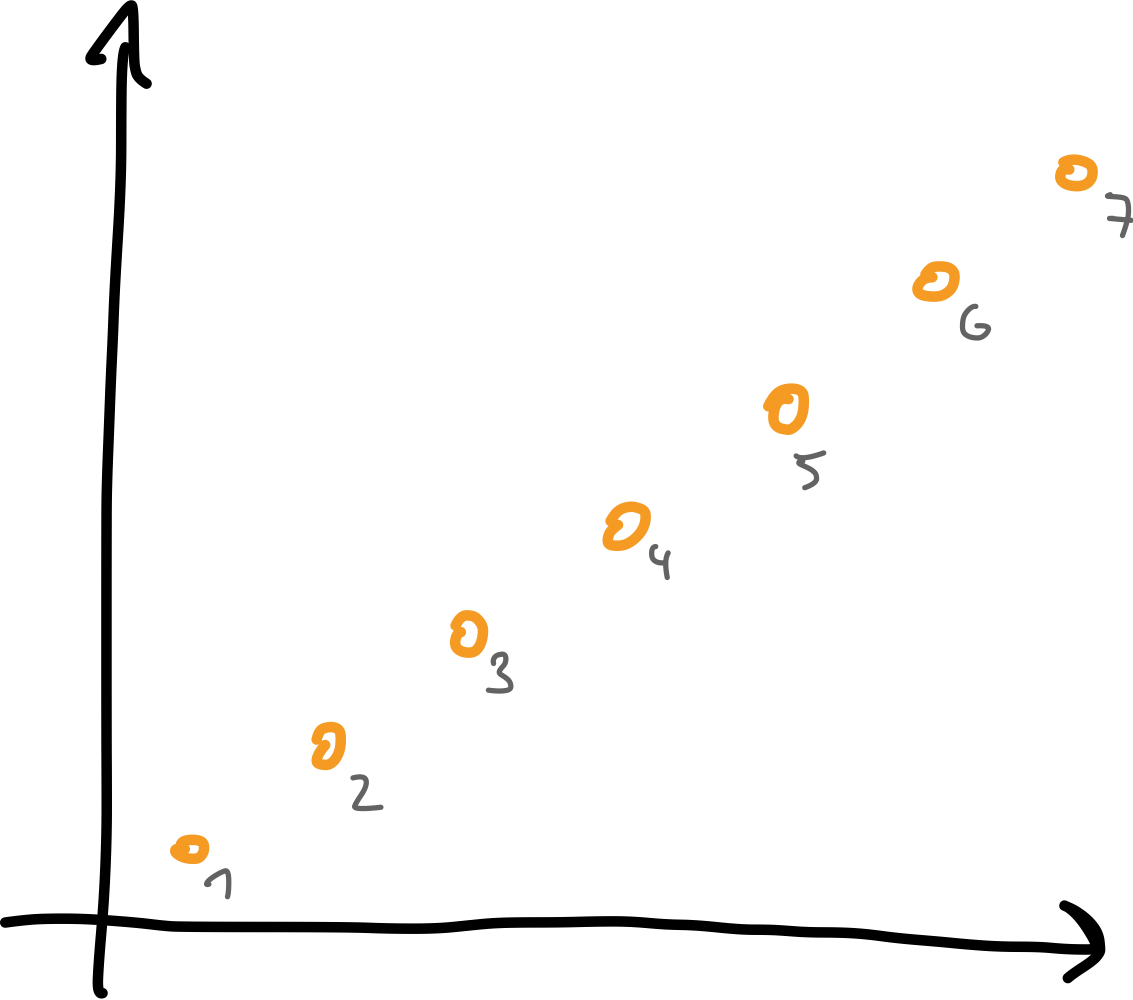
$T(T(\sigma))$

Why does it work?

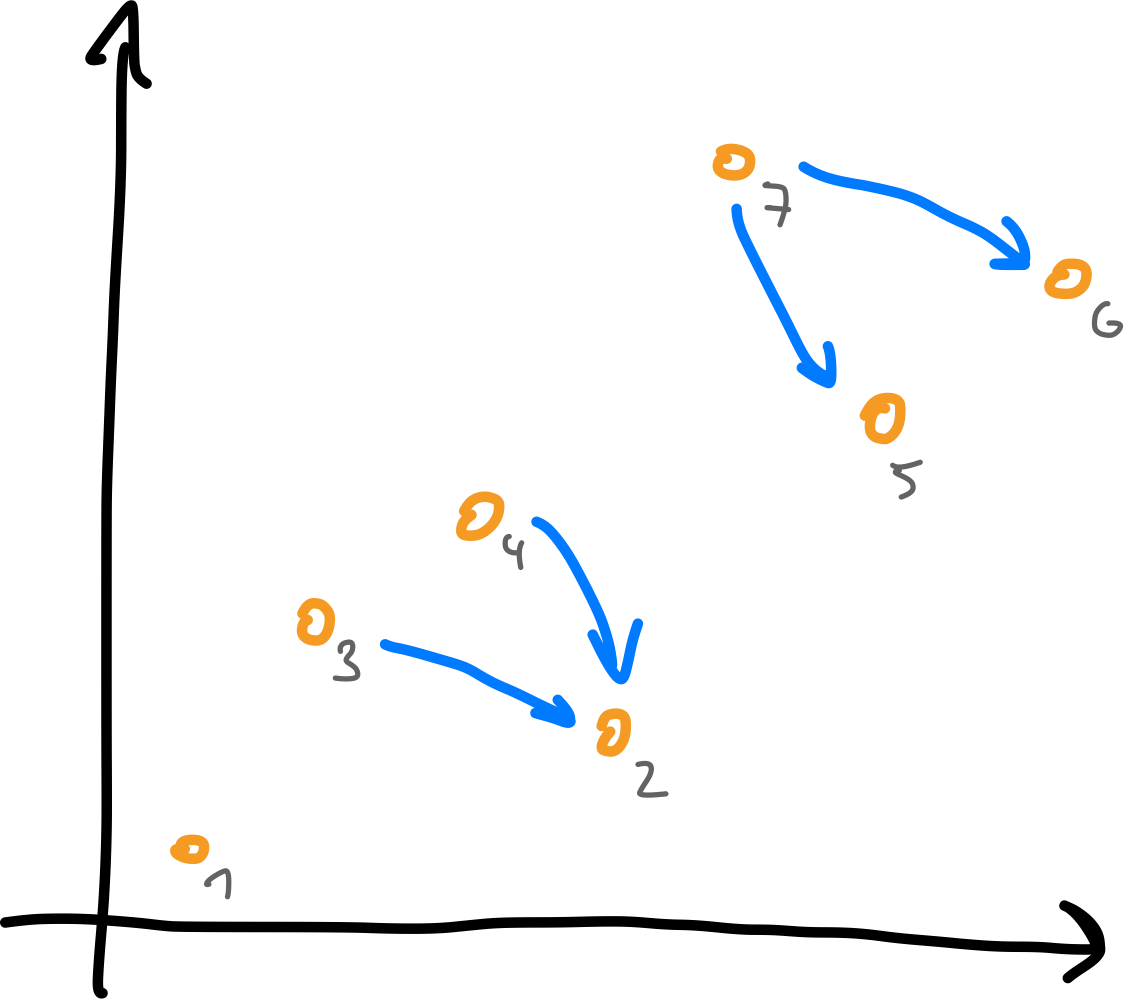
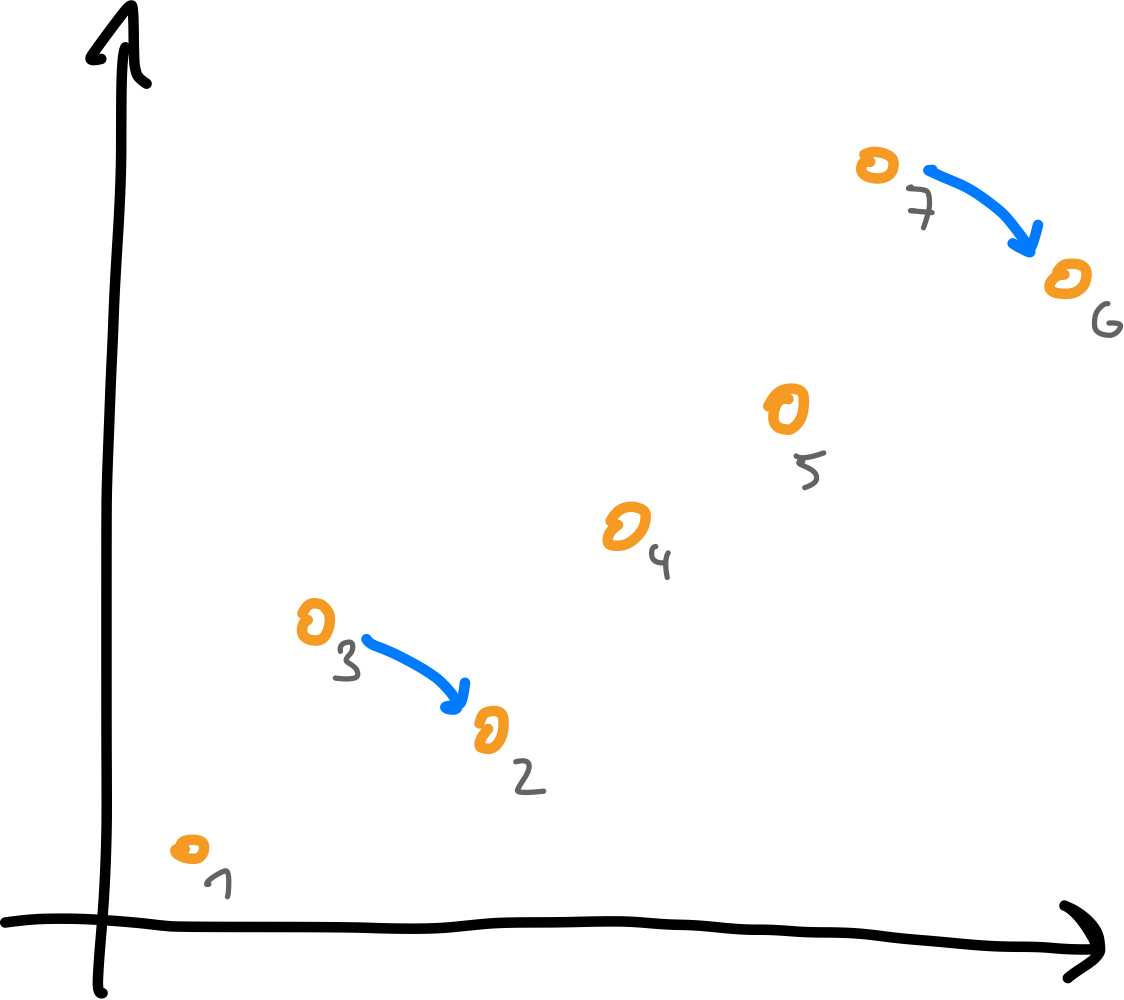
  • Number of inversions is strongly decreasing!
  • At most $\binom{n}{2}$ inversions $\Rightarrow$ sorted after $\leq \binom{n}{2}$ rounds.
Theorem (Ungar, 1982)
Any permutation of $[n]$ is sorted after at most $n-1$ flip-rounds.

The Sorting Tree

  • leaves/non-leaves
  • close to root
  • far away from root

The Sorting Tree

Pop-Stacked Permutations

If flipping some permutation yields $\sigma$, it is called pop-stacked.
Theorem (Asinowski-Banderier-Billey-H.-Linusson, 2019)
A permutation is pop-stacked $\iff$ consecutive runs overlap
  • If runs overlap: reverse-flip yields $\tau$ with $T(\tau) = \sigma$
  • If no overlap: reverse-flip joins two falls $\rightsquigarrow$

Enumerating Pop-Stacked Permutations

Brute force enumeration: 
1, 1, 3, 11, 49, 263, 1653, 11877, 95991, 862047, 8516221, 91782159, ...
  • No success with guessing, no obvious recursive structure
  • Try again, introduce new parameter for number of runs!
Theorem (Asinowski-Banderier-Billey-H.-Linusson, 2019)
The number of pop-stacked permutations with $k$ runs is a $C$-finite sequence(satisfies a linear recurrence with constant coefficients / has a rational generating function).

Enumerating Pop-Stacked Permutations

Theorem (Asinowski-Banderier-Billey-H.-Linusson, 2019)
The number of pop-stacked permutations with $k$ runs is a $C$-finite sequence(satisfies a linear recurrence with constant coefficients / has a rational generating function).
Bijection: permutations with $k$ runs $\leftrightarrow$ $\cal{L}_k \subset $ words over $[k]$
\[ 261453 \mapsto 213221 \]

Enumerating Pop-Stacked Permutations

Bijection: permutations with $k$ runs $\leftrightarrow$ $\cal{L}_k \subset $ words over $[k]$
  • Construct automaton recognizing $\cal{L}_k$!
  • $\cal{L}_k$ is regular!

Enumerating Pop-Stacked Permutations

  • $\cal{L}_k$ is regular!

Generating functions

  • Can be extracted explicitly from automaton...
    Determinants of symbolic matrices of automaton size $\Theta((2 + \sqrt{2})^k)$ involved!
  • ... or guessed from data, as GF is rational.

Enumerating Pop-Stacked Permutations

Generating functions

\[\begin{aligned} P_1(z) &= \frac{z}{1-z}\\ P_2(z) &= \frac{2z^2}{(1-z)^2 (1-2z)}\\ P_3(z) &= \frac{2z^4 (1 + 3z - 6z^2)}{(1-z)^3 (1-2z)^2 (1-3z)}\\ P_4(z) &= \frac{2z^6 (21 - 74z + 5z^2 + 180z^3 - 144z^4)}{(1-z)^4 (1-2z)^3 (1-3z)^2 (1 - 4z)} \end{aligned}\]
Conjecture: $P_k(z) = -1 + \frac{1}{1 - kz} + \sum_{j=1}^{k-1} \frac{\text{poly}_{k, j} (z)}{(1 - (k-j)z)^{j+1}}$

Efficient Enumeration

Idea: Generate pop-stacked permutations by expanding $(1)$ and $(12)$
Expansion rules:
  1. New run of length 1 at end: $13|25|4 \rightsquigarrow 14|26|5|3$
  2. New run of length 2 at end: $13|24 \rightsquigarrow 14|35|26$
  3. New second-largest element in last run: $13|4|25 \rightsquigarrow 14|5|236$
Observe: All permutations are generated: consider the reversal!
  1. If last run is of length 1 or 2: delete it. Then relabel.
  2. Otherwise delete penultimate element. Then relabel.

Efficient Enumeration

Theorem (Asinowski-Banderier-H., 2020)
$p_{N,K;A,B,C}$ ... pop-stacked permutations of $[N]$ with $K$ runs; last run of shape $(A...BC)$. \[\begin{aligned} p_{N,K;A,B,C} = {} & [A = B = C] \sum_{a=1}^{A-1} \sum_{b=1}^{N-1} \sum_{c=A}^{N-1} p_{N-1,K-1;a,b,c} \\ & + [A = B < C] \sum_{a=1}^{C-2} \sum_{b=1}^{N-2} \sum_{c=A}^{N-2} p_{N-2,K-1;a,b,c} \\ & + [A < B < C] \sum_{b = A}^{B-1} p_{N-1, K; A, b, C-1} \end{aligned}\]
  • Pop-stacked permutations with $k$ runs by summing over $a$, $b$, $c$ in $p_{n, k; a, b, c}$ ...
  • ... and all pop-stacked permutations via summation over $k$
    In $\sim n^4/8$ operations requiring $\sim n^3/3$ memory.

Asymptotic Growth

Lemma (Asinowski-Bandierier-Billey-H.-Linusson, 2019)
The number of pop-stacked permutations of size $n$ grows superexponentially.

Intertwining two permutations gives a pop-stacked permutation:

$$\Rightarrow p_{2n} \geq (n!)^2$$

Asymptotic Growth

Conjecture
The number of pop-stacked permutations of size $n$ grows like \[ p_n \sim (0.695688...) \cdot (0.898118...)^n \cdot n! \] for $n\to\infty$, and the generating function is not holonomic.
Rigorous numerical experiments + alternative generation algorithm in [Claesson, Guðmundsson, Pantone].

Low-cost Permutations

Permutation $\sigma$ is $k$-pop-stack-sortable if $T^k(\sigma) = \id$.
Known results:
  • $T(\sigma) = \id$ if and only if $\sigma$ is layered(a direct sum of falls), [Avis–Newborn]
  • Structural characterization of $2$-pop-stack-sortable permutations and bijection to polyominoes on a twisted cylinder, [Pudwell–Smith]
  • For fixed $k$: generating function of $k$-pop-stack-sortable permutations is rational, [Claesson–Guðmundsson]

Low-cost Permutations

Theorem (Asinowski-Banderier-H., 2020)
Pop-stacked $1$-pop-stack-sortable permutations are enumerated by the generating function
\[ x + \frac{(x + x^2)^2}{1 - (x + x^2 + x^3)} = x + x^2 + 3x^3 + 5x^4 + 9x^5 + 17x^6 + \dots, \]
that is, by tribonacci numbers.
Layered permutations have overlapping runs if...
  • there are two outer falls of length 1 or 2 $\rightsquigarrow (x + x^2)^2$
  • and if all inner falls are of length 1, 2, or 3 $\rightsquigarrow \frac{1}{1 - (x + x^2 + x^3)}$

Low-cost Permutations

$a_{n,k} \dots$ # of 2-pop-stack-sortable permutations of size $n$ with $k$ ascents

Theorem (Asinowski-Banderier-H., 2020)
  1. $\displaystyle \sum_{n,k \geq 0} a_{n,k} x^n y^k = \frac{x (1 + x^2 y)}{1 - x - xy - x^2 y - 2x^3 y^2}$
  2. For fixed $k$:
    $\displaystyle \sum_{n \geq 0} a_{2n+k+1,n+k} x^n = \sqrt{\frac{1 + x}{1 - 7x}} \left(\frac{1 - x - \sqrt{(1+x)(1-7x)}}{2x}\right)^k$

Low-cost Permutations

$a_{n,k} \dots$ # of 2-pop-stack-sortable permutations of size $n$ with $k$ ascents

  • Use: 2-pop-stack-sortable $\iff$ adjacent falls $\max(F_i) \leq \min(F_{i+1}) + 1$
  • Bijection of these permutations to two-colored lattice paths:

High-cost Permutations

Bandwidth: $\displaystyle d(a_1 a_2 \dots a_n) = \max_{i} |a_i - i|$.

Theorem (Asinowski–Banderier–H., 2020)
Let $0\leq m\leq n-1$. If $\pi\in \operatorname{Im}(T^m)$, then $d(\pi) \leq n - 1 - m$.

High-cost Permutations

Theorem (Asinowski–Banderier–H., 2020)
Let $0\leq m\leq n-1$. If $\pi\in \operatorname{Im}(T^m)$, then $d(\pi) \leq n - 1 - m$.

High-cost Permutations

Theorem (Asinowski–Banderier–H., 2020)
Let $0\leq m\leq n-1$. If $\pi\in \operatorname{Im}(T^m)$, then $d(\pi) \leq n - 1 - m$.

Proof idea: careful investigation of wiring diagrams + establish skew-layered permutations with two runs as extremal cases.

High-cost Permutations

Permutation $\pi$ is thin if $d(\pi) \leq 1$. Thin permutations are determined by number and length of their runs.

Theorem (Asinowski–Banderier–H., 2020)

$\pi \in \operatorname{Im}(T^{n-2}) \iff {}$ $\pi$ is thin and has no inner runs of odd size.

There are $2^{n/2 - 1} + 2^{n/2} - 1$ and $2^{(n+1)/2} - 1$ such permutations for even and odd $n$, respectively.

High-cost Permutations

Via characterization of $\operatorname{Im}(T^{n-2})$:
skew-layered permutations without odd inner runs need $n-1$ flips.

Conjectures. Let $\pi$ be skew-layered of size $n$, not $\id$ and not $-\id$.
  • For even $n$, $\pi$ needs $n-1$ flips to be sorted.
  • For odd $n$, if the middle element is also the center of a run or fall of size $\geq 3$, then $\pi$ needs $n-2$ flips. Otherwise it needs $n-1$ flips.

Thank you!